Have you ever wondered how to determine whether an investment is worth pursuing or which project offers the best return? The Internal Rate of Return (IRR) is a powerful tool that can help you answer these questions with confidence. IRR measures the profitability of an investment by calculating the rate at which the net present value (NPV) of future cash flows equals zero. It provides a clear percentage that represents the expected return, making it easier to compare different investments and assess their potential.
This guide will walk you through the essentials of IRR, from its basic definition to advanced concepts, offering practical insights and tips to help you make more informed financial decisions. Whether you’re evaluating investment opportunities, analyzing projects, or comparing business ventures, understanding IRR can give you a clearer picture of potential returns and help you choose wisely.
What is IRR?
The Internal Rate of Return (IRR) is a key financial metric used to evaluate the profitability of an investment or project. It represents the discount rate at which the Net Present Value (NPV) of all future cash flows—both inflows and outflows—equals zero. Essentially, IRR is the rate of return that makes an investment break even in terms of its NPV.
To put it simply, IRR is the percentage rate that makes the present value of expected cash flows equal to the initial investment. It’s an essential tool for investors and financial analysts to assess the efficiency and potential profitability of different investment opportunities.
How IRR Is Calculated
IRR is determined through a process of iterative calculations that involve solving the following equation:
0 = ∑ (Cash Flow / (1 + IRR)^t) - Initial Investment
Where:
- Cash Flow represents the net inflows or outflows at each time period.
- IRR is the rate you’re solving for.
- t is the time period of each cash flow.
The calculation typically requires financial software or a financial calculator, as solving this equation manually can be complex and time-consuming due to its iterative nature.
Importance of IRR in Financial Analysis
Understanding the significance of IRR in financial analysis can greatly enhance your investment decision-making process. Here’s why IRR is crucial:
- Quantifies Investment Return: IRR provides a clear percentage that represents the expected annual return on an investment. This makes it easier to understand and compare the profitability of various investment opportunities.
- Facilitates Comparison: By converting different investments into a percentage return, IRR allows you to directly compare projects of different sizes and durations. This helps in evaluating which investment offers the best return relative to its cost.
- Incorporates Time Value of Money: Unlike simple return measures, IRR accounts for the time value of money, ensuring that future cash flows are appropriately discounted. This provides a more accurate picture of an investment’s true profitability.
- Decision-Making Tool: IRR helps in making informed investment decisions by setting a clear benchmark. If the IRR exceeds your required rate of return or the cost of capital, it indicates a potentially worthwhile investment.
- Risk Assessment: IRR can aid in assessing the risk associated with an investment. A higher IRR often signifies a higher return potential, but it should be evaluated alongside other factors like project risk and market conditions to ensure a balanced analysis.
Incorporating IRR into your financial analysis allows you to make more informed and strategic investment decisions, ultimately enhancing the potential for achieving favorable financial outcomes.
Theoretical Background of IRR
Understanding the theoretical background of IRR helps you grasp its practical applications and limitations. This section explores key concepts such as the time value of money, IRR’s relationship with NPV, and how it compares to other financial metrics.
Concept of Time Value of Money
The time value of money (TVM) is a cornerstone of financial theory. It posits that a dollar today is worth more than a dollar in the future due to its potential earning capacity. This principle is crucial for understanding IRR because it fundamentally influences how future cash flows are evaluated.
Here’s why TVM matters:
- Opportunity Cost: Money available today can be invested to earn a return. Thus, $100 today is worth more than $100 received a year from now because you could potentially earn interest on the $100 today.
- Discounting Future Cash Flows: IRR incorporates TVM by discounting future cash flows to their present value. This ensures that cash flows received later in time are appropriately valued less than those received sooner.
Example: Suppose you receive $1,000 today versus $1,000 in three years. If you invest the $1,000 today at an annual interest rate of 5%, it will grow to $1,157.63 in three years. Thus, receiving $1,000 today is more valuable because of the potential interest earnings.
How IRR Relates to Net Present Value (NPV)
IRR and NPV are interconnected financial metrics that help assess the profitability of investments. While they are related, they offer different perspectives.
- Net Present Value (NPV) measures the value of an investment by calculating the present value of all expected cash flows (both inflows and outflows) and subtracting the initial investment. The formula is:
NPV = ∑ (Cash Flow / (1 + r)^t) - Initial Investment
Where:
- Cash Flow = Net inflows or outflows at each period
- r = Discount rate (cost of capital or IRR in some cases)
- t = Time period
If NPV is positive, it indicates that the investment is expected to generate more cash than the cost of capital, making it a profitable venture.
- Internal Rate of Return (IRR) is the discount rate that makes the NPV of all cash flows equal to zero. Essentially, IRR is the rate at which the present value of future cash flows equals the initial investment. It’s the break-even rate of return.To find IRR, solve the equation:
0 = ∑ (Cash Flow / (1 + IRR)^t) - Initial Investment
If IRR exceeds your required rate of return, the investment is considered worthwhile. Conversely, a lower IRR suggests that the investment may not meet your return expectations.
Example: If an investment has an IRR of 12% and your required rate of return is 8%, the investment is attractive as it offers a higher return than your benchmark.
IRR vs Other Financial Metrics
IRR is just one of several metrics used to evaluate investments. Here’s how it compares with other common financial metrics:
- Return on Investment (ROI): ROI measures the profitability of an investment relative to its cost. It is calculated as:
ROI = (Net Profit / Cost of Investment) * 100%
ROI doesn’t consider the time value of money or the timing of cash flows. While it provides a quick measure of profitability, it lacks the depth that IRR offers.
- Payback Period: This metric indicates how long it takes to recover the initial investment. It’s calculated as:
Payback Period = Initial Investment / Annual Cash Inflows
The payback period is simple but ignores cash flows after the payback period and doesn’t account for the time value of money.
- Profitability Index (PI): PI is the ratio of the present value of future cash flows to the initial investment. It’s calculated as:
PI = (Present Value of Future Cash Flows / Initial Investment)
A PI greater than 1 indicates a good investment. PI, like NPV, considers the time value of money but is less intuitive than IRR.
- Discounted Cash Flow (DCF): DCF is a valuation method used to estimate the value of an investment based on its future cash flows, discounted back to their present value. It’s closely related to IRR and NPV but provides a more comprehensive analysis when combined with these metrics.
Each metric has its strengths and limitations. While IRR provides a percentage return and considers the time value of money, other metrics like ROI and Payback Period offer simpler, more direct insights. Combining IRR with these other metrics can give a more rounded view of an investment’s potential.
How to Calculate IRR?
Calculating the Internal Rate of Return (IRR) can seem complex, but breaking it down into its components makes the process more manageable. This section covers the mathematical formula for IRR, the importance of understanding cash flows, the use of financial calculators and software, and the manual calculation methodology.
IRR Formula
The mathematical formula for IRR involves finding the discount rate that sets the Net Present Value (NPV) of cash flows to zero. Here’s how it works:
The general equation for NPV, set to zero for IRR calculations, is:
0 = ∑ (Cash Flow / (1 + IRR)^t) - Initial Investment
Where:
- Cash Flow represents the net inflows or outflows at each period.
- IRR is the Internal Rate of Return you need to find.
- t is the time period of each cash flow.
To solve for IRR, you essentially need to find the rate that makes the sum of the present values of all future cash flows equal to the initial investment. Because IRR calculation involves solving this equation, it usually requires iterative methods or financial software.
Example: Suppose you invest $1,000 today and expect to receive $400 annually for five years. To calculate IRR, you need to find the rate at which the present value of these $400 payments equals $1,000.
Understanding Cash Flows
Cash flows are the cornerstone of IRR calculations. They represent the money that goes in and out of an investment or project over time. Accurate cash flow estimation is crucial for determining IRR effectively.
- Initial Investment: This is the amount of money invested upfront. It’s usually a negative cash flow since it represents an outflow.
- Future Inflows: These are the positive cash flows expected from the investment. They can be periodic, such as annual returns, or lump sums at specific intervals.
- Future Outflows: Additional costs or investments required during the life of the project. These are also negative cash flows.
Example: For a project requiring an initial investment of $5,000 and generating annual cash inflows of $1,200 for five years, you need to account for these inflows and compare them against the initial investment to determine the IRR.
Using Financial Calculators and Software
Modern technology simplifies IRR calculations. Financial calculators and software like Excel can perform complex IRR computations quickly and accurately.
Using Financial Calculators:
- Input Cash Flows: Enter the initial investment and subsequent cash flows into the calculator.
- Compute IRR: Most financial calculators have an IRR function that will iterate through possible rates to find the one that sets NPV to zero.
Using Excel: Excel offers a built-in IRR function that simplifies the process:
=IRR(values, [guess])
- values: Array of cash flows, including the initial investment.
- [guess]: Optional estimate of IRR to help the function start its iterations.
Example: If you input -5000 for the initial investment and 1200 for each of the five years as inflows, Excel will calculate the IRR based on these values.
Manual Calculation Methodology
Calculating IRR manually is more challenging and involves trial and error. It requires guessing different discount rates to find the one that makes NPV zero. Here’s how to approach it:
- Estimate Initial IRR: Start with an estimated rate of return. This could be a rough guess based on similar projects or past experiences.
- Calculate NPV: Use the estimated IRR to calculate NPV using the formula:
NPV = ∑ (Cash Flow / (1 + r)^t) - Initial Investment
Adjust r to find the rate that brings NPV close to zero.
- Refine Estimates: Iterate with different rates, adjusting until you find the IRR where NPV equals zero.
Example: For an investment with an initial outflow of $5,000 and inflows of $1,200 each year for five years, you might start with an IRR guess of 8%. Calculate NPV with this rate. If NPV is positive, increase the rate and recalculate. If NPV is negative, decrease the rate. Repeat until you find the rate that zeroes out NPV.
Manually calculating IRR is time-consuming and prone to errors, which is why most financial professionals rely on calculators and software for accuracy.
IRR Applications
IRR is a versatile metric used in various financial scenarios to assess the viability and profitability of investments and projects. Understanding how to apply IRR effectively can help you make informed decisions about where to allocate resources. This section explores how IRR is used in investment appraisal, project evaluation, comparing investment opportunities, and assessing business ventures.
Investment Appraisal
Investment appraisal involves evaluating the attractiveness of an investment or project. IRR is a key metric in this process because it provides a straightforward percentage return on the investment. When you’re appraising an investment, you compare its IRR to your required rate of return or the cost of capital.
If the IRR exceeds the cost of capital, it suggests that the investment is likely to generate returns above the minimum required, making it a potentially lucrative opportunity. Conversely, if the IRR is lower than the cost of capital, the investment might not be worthwhile, as it may not meet your return expectations.
Project Evaluation
Project evaluation focuses on determining whether a specific project is worth undertaking. IRR is instrumental in this process as it helps quantify the potential returns of a project relative to its costs.
Projects with higher IRRs are generally more attractive, as they indicate better profitability relative to their cost. However, it’s essential to consider IRR in conjunction with other factors, such as project risk, size, and duration, to ensure a comprehensive evaluation. Projects with similar IRRs might differ significantly in their risk profiles or capital requirements, which can impact your decision.
Comparing Investment Opportunities
When faced with multiple investment options, IRR helps you compare and choose the most promising opportunity. By calculating and comparing the IRR of different investments, you can identify which one offers the best return on your capital.
While IRR is a useful comparison tool, it’s important to remember that it doesn’t account for the scale of the investment. A higher IRR might not always mean a better investment if the scale of the investment is significantly different. For instance, a small investment with a high IRR might offer lower absolute returns compared to a larger investment with a slightly lower IRR.
Assessing Business Ventures
For assessing new business ventures, IRR helps evaluate the potential return on investment relative to the initial funding required. Business ventures often involve various cash inflows and outflows, and calculating IRR provides insight into the overall profitability of the venture.
A business venture with a higher IRR is generally more appealing, as it suggests a higher return relative to the initial investment. However, it’s crucial to also consider other aspects such as market conditions, competitive landscape, and strategic alignment with your business goals. IRR provides a financial perspective, but a comprehensive assessment includes evaluating qualitative factors and potential risks.
Understanding how to apply IRR in these contexts enables you to make well-informed financial decisions, ensuring that your investments and projects align with your financial goals and risk tolerance.
Examples of IRR in Practice
Understanding IRR is much clearer with practical examples. Here, we’ll explore various scenarios to illustrate how IRR can be applied to different types of investments and projects. These examples will help you see how IRR works in real-world situations and how to interpret the results effectively.
Example 1: Evaluating a New Product Launch
Imagine you’re considering investing in a new product launch for your company. You expect the following cash flows over the next five years:
- Initial Investment: $500,000
- Year 1: $100,000
- Year 2: $150,000
- Year 3: $200,000
- Year 4: $250,000
- Year 5: $300,000
To find the IRR, you need to solve the equation where the net present value (NPV) of these cash flows equals zero. Using a financial calculator or Excel, you input these cash flows to compute the IRR.
Assuming you calculate an IRR of 12%, this means the project is expected to yield a 12% annual return. If your company’s required rate of return or cost of capital is 10%, this project is considered attractive as it exceeds your benchmark.
Example 2: Comparing Two Investment Opportunities
Suppose you have two investment opportunities, each requiring different initial investments and generating different cash flows. Here’s a summary of both options:
- Investment A:
- Initial Investment: $200,000
- Year 1: $50,000
- Year 2: $60,000
- Year 3: $70,000
- Year 4: $80,000
- Investment B:
- Initial Investment: $150,000
- Year 1: $40,000
- Year 2: $60,000
- Year 3: $80,000
- Year 4: $100,000
By calculating the IRR for both investments, you find that Investment A has an IRR of 14%, while Investment B has an IRR of 16%. Although Investment B offers a higher percentage return, you should also consider the scale of the investments and total return in your final decision. If Investment B’s absolute returns align better with your goals and risk tolerance, it may be the preferable choice despite the smaller initial investment.
Example 3: Assessing a Business Expansion Project
You’re evaluating a business expansion project with the following expected cash flows:
- Initial Investment: $1,000,000
- Year 1: $200,000
- Year 2: $250,000
- Year 3: $300,000
- Year 4: $350,000
- Year 5: $400,000
After calculating the IRR, you find it to be 11%. This IRR reflects the expected return from expanding your business. If your company’s cost of capital is 9%, the project is deemed profitable since the IRR exceeds your required rate of return.
Example 4: Analyzing a Real Estate Investment
Consider a real estate investment where you purchase a property with the following financial details:
- Initial Purchase Price: $800,000
- Annual Rental Income: $100,000
- Year 5 Sale Price: $1,000,000
Assuming the property generates consistent rental income and is sold for $1,000,000 at the end of Year 5, the IRR calculation will consider both the rental income and the sale proceeds.
By calculating the IRR, you determine it is 9%. This percentage shows the annualized return on the investment, incorporating both rental income and the gain from selling the property. Comparing this IRR to other real estate opportunities or investment options can help you decide if this investment meets your financial goals.
These examples illustrate how IRR can be applied in various scenarios to assess investment potential and make informed financial decisions. By understanding the IRR results in each case, you can better evaluate and compare different opportunities to optimize your investment strategy.
Advantages of Using IRR
IRR is a widely-used financial metric with several key advantages that make it valuable for evaluating investments and projects. Here’s a look at the benefits of using IRR:
- Simplicity and Intuitiveness: IRR provides a single percentage that represents the expected return on an investment, making it easy to understand and communicate. It simplifies the evaluation process by offering a clear, straightforward measure of profitability.
- Comparison of Different Projects: IRR allows you to compare investments or projects of varying sizes and durations on a common scale. By standardizing returns, IRR helps you assess which projects or investments offer the best relative return.
- Incorporation of Time Value of Money: Unlike metrics that do not account for the time value of money, IRR includes this principle by discounting future cash flows. This provides a more accurate measure of an investment’s potential profitability.
- Decision-Making Ease: IRR can streamline decision-making processes by providing a clear threshold. If the IRR exceeds the cost of capital or required rate of return, it indicates a potentially worthwhile investment, simplifying the decision-making process.
IRR Limitations and Challenges
While IRR is a useful metric, it does come with certain limitations and challenges that can affect its reliability and applicability. Here are some of the key issues:
- Assumptions Behind IRR: IRR assumes that all intermediate cash flows are reinvested at the same rate as the IRR itself. In reality, reinvestment rates might differ, which can skew the accuracy of the IRR calculation.
- Multiple IRRs: Projects with non-conventional cash flows—where cash flows alternate between positive and negative—can result in multiple IRRs. This situation complicates the interpretation of the IRR, as it’s challenging to determine which rate is most relevant.
- Scale and Size of Investment: IRR doesn’t consider the scale of the investment. A small project with a high IRR might not generate as much total return as a larger project with a lower IRR, which can mislead investors if not considered alongside other metrics.
- Sensitivity to Cash Flow Variations: IRR can be sensitive to fluctuations in cash flows. Small changes in projected cash flows can significantly impact the IRR, potentially making it less reliable for investments with uncertain or variable cash flows.
- Limited Insight into Project Duration: IRR does not provide information about the length of the project or investment. Two projects with the same IRR but different durations might have different implications for cash flow timing and overall financial impact.
Understanding these limitations is crucial for effectively using IRR as part of a comprehensive financial analysis. Combining IRR with other metrics and considerations can provide a more complete picture of an investment’s potential.
Advanced IRR Concepts
Exploring advanced IRR concepts can provide deeper insights into the metric and address some of its limitations. These advanced concepts include the Modified Internal Rate of Return (MIRR), the distinction between Real and Nominal IRR, handling non-conventional cash flows, and employing sensitivity analysis for better decision-making.
Modified Internal Rate of Return (MIRR)
The Modified Internal Rate of Return (MIRR) refines the traditional IRR calculation by addressing some of its limitations. Unlike IRR, which assumes reinvestment of cash flows at the same rate as the IRR itself, MIRR uses a more realistic approach to reinvestment and financing rates.
MIRR is calculated using the following formula:
MIRR = (Future Value of Positive Cash Flows / Present Value of Negative Cash Flows)^(1/n) - 1
Where:
- Future Value of Positive Cash Flows: Calculated using the reinvestment rate.
- Present Value of Negative Cash Flows: Discounted using the finance rate.
- n: Number of periods.
MIRR provides a more accurate measure of an investment’s profitability by assuming that positive cash flows are reinvested at a specified rate and negative cash flows are financed at another specified rate. This approach helps mitigate the issues of multiple IRRs and unrealistic reinvestment assumptions.
Real IRR versus Nominal IRR
Understanding the difference between Real IRR and Nominal IRR is crucial for accurate financial analysis.
- Nominal IRR: This is the IRR calculated without adjusting for inflation. It reflects the return in current dollars and does not account for changes in purchasing power over time.
- Real IRR: Real IRR adjusts for inflation, providing a measure of the return in constant dollars. This adjustment helps in understanding the true value of returns after accounting for changes in the inflation rate.
To calculate Real IRR, you use the following formula:
Real IRR = (1 + Nominal IRR) / (1 + Inflation Rate) - 1
This distinction is important because Nominal IRR can be misleading if inflation is high. Real IRR offers a clearer picture of the investment’s actual purchasing power and economic return.
IRR for Non-Conventional Cash Flows
Non-conventional cash flows involve alternating between positive and negative cash flows, which can complicate IRR calculations. These types of cash flows can result in multiple IRRs or no IRR at all, making interpretation challenging.
To handle non-conventional cash flows:
- Multiple IRRs: If a project generates multiple IRRs, consider using MIRR or NPV for a more reliable evaluation. Multiple IRRs can create confusion as they represent different rates that satisfy the NPV equation.
- No IRR: If cash flows are such that no IRR exists, NPV and other metrics like profitability index or discounted payback period may be more appropriate for assessing the investment.
Adjustments to the traditional IRR calculation or the use of alternative metrics can provide better insights into the viability of projects with complex cash flow patterns.
Sensitivity Analysis and Scenario Planning
Sensitivity analysis and scenario planning are advanced techniques that help in understanding how changes in assumptions impact the IRR and overall investment outcomes. These methods provide a more comprehensive view of risk and uncertainty.
- Sensitivity Analysis: This involves varying key assumptions, such as cash flows or discount rates, to see how changes affect the IRR. Sensitivity analysis helps identify which variables have the most significant impact on the investment’s profitability.
- Scenario Planning: This method examines different scenarios—best case, worst case, and most likely case—to assess how different conditions might affect the IRR. Scenario planning helps in preparing for various possible outcomes and understanding the range of potential returns.
By applying sensitivity analysis and scenario planning, you can better gauge the robustness of an investment’s return and make more informed decisions under uncertainty. These techniques enhance the reliability of IRR by considering the variability in assumptions and potential risks.
Conclusion
Understanding the Internal Rate of Return (IRR) is essential for making sound financial decisions. By providing a percentage that reflects the expected return on an investment, IRR simplifies the process of evaluating and comparing different opportunities. Whether you’re assessing new projects, comparing potential investments, or analyzing business ventures, IRR offers a clear metric to gauge profitability and ensure that your investments align with your financial goals. It incorporates the time value of money, giving you a more accurate picture of how future cash flows contribute to your overall return.
However, it’s important to remember that IRR is just one tool in your financial toolbox. While it provides valuable insights, it comes with limitations and should be used alongside other metrics like NPV, ROI, and sensitivity analysis for a comprehensive evaluation. By considering these factors together, you can make well-rounded decisions that reflect both the potential returns and the inherent risks of your investments. Armed with a solid understanding of IRR and its applications, you’re better equipped to navigate the complexities of investment analysis and optimize your financial strategy.
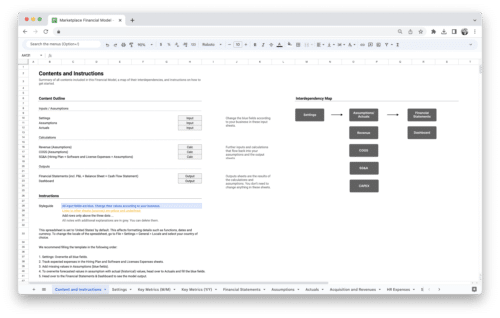
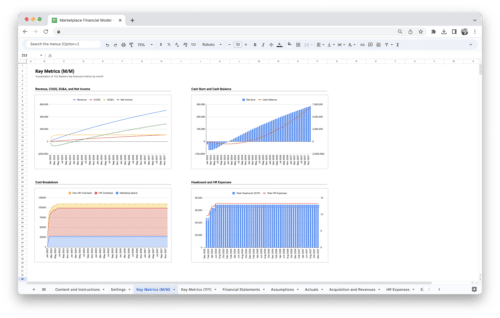
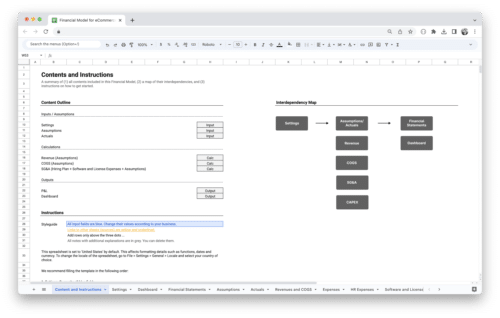
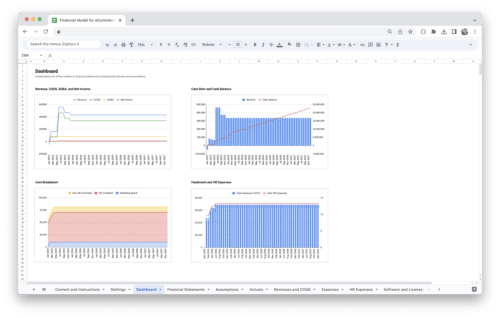
Get Started With a Prebuilt Template!
Looking to streamline your business financial modeling process with a prebuilt customizable template? Say goodbye to the hassle of building a financial model from scratch and get started right away with one of our premium templates.
- Save time with no need to create a financial model from scratch.
- Reduce errors with prebuilt formulas and calculations.
- Customize to your needs by adding/deleting sections and adjusting formulas.
- Automatically calculate key metrics for valuable insights.
- Make informed decisions about your strategy and goals with a clear picture of your business performance and financial health.